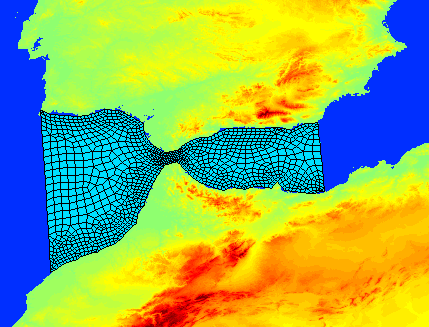
Sobre el océano

Nota al lector: El presente texto representa únicamente una pequeña reflexión personal sobre la materia. En ningún momento pretende ser un texto científico con rigor, tan sólo unas pequeñas notas a título informativo para aquel a quien pueda interesar.

Los modelos de oceanografía

El punto de partida para cualquier modelo de océano son las ecuaciones de Navier-Stokes en un sistema de referencia que está en movimiento de rotación con una velocidad angular $\vec{\Omega}$ (la rotación de la Tierra).

En concreto, las ecuaciones vienen dadas por: \[ \begin{cases} \rho{\displaystyle \frac{D\vec{u}}{Dt}}-\mbox{div}\left(\nu\nabla\vec{u}\right)+2\vec{\Omega}\times\vec{u}=-\nabla p+\rho\vec{g}, & \mbox{ en }D,\\ \mbox{div}\vec{u}=0, & \mbox{ en }D,\\ +CC \end{cases} \] donde

$\vec{u}=\left(u,v,w\right)$ es la velocidad del fluido,
$p$ es la presión,
$\rho$ es la densidad,
$\nu$ es la viscosidad,
$\vec{g}$ es vector gravedad,
$\vec{\Omega}$ la velocidad angular que, en este caso verifica que $\left|\vec{\Omega}\right|=2\pi\mbox{ rad}/\mbox{día}=7.2722\times10^{-5}\mbox{ rad}/\mbox{s}$,

y por último, $D$ es el dominio, que físicamente corresponde con la región de estudio. Por ejemplo, si pensamos en realizar un estudio en el Mar Mediterráneo, nuestro dominio $D$ sería un subconjunto del espacio, es decir, $D\subset\mathbb{R}^{3}$, con la geometría y las dimensiones del Mar Mediterráneo, es decir:

Debido a las particularidades del océano, existe una serie de simplificaciones que se pueden hacer:

Superficie libre o superficie rígida

La superficie del océano está en constante movimiento, por tanto, el dominio $D$ en realidad no es fijo y varia a lo largo del tiempo. los modelos de océano se dividen en modelos de superficie libre o modelos de superficie rígida. Los primeros modelizan el océano permitiendo el movimiento de la superficie mientras que los segundos imponen la condición de que la superficie del océano no se mueve. Si bien los modelos de superficie libre son más realistas, los modelos de superficie rígida son una buena aproximación ya que las variaciones de la superficie del oceáno son del orden del metro frente al orden de los mil metros en la escala vertical del dominio (la profundidad característica). En cualquier caso, en ciertas regiones del océano en las que las variaciones en el nivel del mar son importantes, los modelos de superficie libre son esenciales, o bien, utilizar algún tipo de parametrización en modelos de superficie rígida que simulen el movimiento de la superficie del océano.

La geometría de la superficie: proyecciones

La superficie del océano, salvando el posible movimiento de ésta, se puede considerar esférica, es decir, es un trozo de esfera. Proyección del plano-$\beta$, proyecciones cónicas. Vector $\vec{g}$.

La viscosidad

Anisotropía

La densidad

Procesos que intervienen en el cambio de densidad, introducción de las ecuaciones de temperatura y salinidad

La aproximación hidrostática

Anterior | Inicio | Siguiente

Mallado de la superficie del océano en la región del Estrecho de Gibraltar

Mallado 3D del océano en la región del Estrecho de Gibraltar utilizando hexaedros

Modelización de una batería de ion de litio

Contacto: Dpto. Matemáticas del Área Industrial, E.T.S. Ingenieros Industriales. C/ José Gutierrez Abascal, 2, 28006 Madrid - Spain
Tlfn: (+34) 91 06 77369 / fax: (+34) 91 336 3001 / email: pedro.galan@upm.es