
Dpto. Matemática Aplicada a la Ingeniería Industrial
E.T.S. Ingenieros Industriales
Profesor Contratado Doctor

|
Dpto. Matemática Aplicada a la Ingeniería Industrial Profesor Contratado Doctor |
Algunas simulacionesLas siguientes simulaciones numéricas son un primer paso para un modelo de océano no hidrostático en el que estamos trabajando. Resuelven un fluido bidimensional que suponemos incompresible y con densidad variable que depende de la temperatura y la salinidad. En lo que sigue, $\vec{u}=\left(u,w\right)$ es la velocidad del fluido, $T$ la temperatura, $S$ la salinidad, $p$ la presión y $\rho$ la densidad. Además, la dinámica del fluido dependerá de su viscosidad, $A$, y la difusión de la temperatura y la salinidad, $K$, que vienen dadas por \[ A=\left(\begin{array}{cc} A_{h} & 0\\ 0 & A_{v} \end{array}\right)\quad\mbox{y}\quad K=\left(\begin{array}{cc} k_{h} & 0\\ 0 & k_{v} \end{array}\right) \] Las ecuaciones, validas en el conjunto $D$ con frontera $\partial D=\overline{\Gamma_{s}\cup\Gamma_{b}\cup\Gamma_{l}}$ (ver figura más abajo),
son las siguientes:
La solución numérica ha sido realizada utilizando el método de elementos finitos junto con esquemas Lagrange-Galerkin. Los detalles se pueden consultar en la siguiente referencia: Galán del Sastre, P., Bermejo, R. Commun. Comput. Phys., 2011. Un primer experimentoEn este primer experimento encerramos un fluido en el dominio $D$ con las siguientes características:
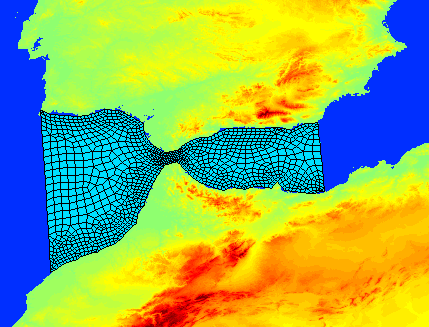
y utilizamos unas condiciones iniciales de flujo en reposo, temperatura constante de $18^{\circ}$ C y tres zonas con distinta salinidad, con valores de $39.2$, $24.1$ y $5.0$ psu. En estas simulaciones utilizamos $A_{h}=A_{v}=10^{-3}$ $\mbox{m}^{2}\mbox{s}^{-1}$ y $k_{h}=k_{v}=10^{-5}$ $\mbox{m}^{2}\mbox{s}^{-1}$ en una primera simulación (izquierda) y $A_{h}=A_{v}=10^{-4}$ $\mbox{m}^{2}\mbox{s}^{-1}$ y $k_{h}=k_{v}=10^{-5}$ $\mbox{m}^{2}\mbox{s}^{-1}$ en una segunda simulación (derecha). Las simulaciones están realizadas con elementos finitos con polinomios de grado $6$. Ajuste gravitacionalEste es un test que se utiliza para validar los modelos de océano, pues pretende reproducir de forma simplificada la dinámica que ocurre en muchos estrechos, como por ejemplo el estrecho de Gibraltar. La idea es generar un canal, en nuestro caso de $64$ km de largo y $20$ m de profundidad, con dos fluidos con distinta densidad separados inicialmente con una membrana que se elimina para que ambos fluidos interactúen. En concreto los dos fluidos presentan una diferencia de densidad de $5$ $\mbox{kg m}^{-3}$ que se se simula mediante una condición inicial para la temperatura constante en todo el dominio de $20^{\circ}$ C y una condición inicial para la salinidad de $30$ y $36.5605$ psu en las dos mitades del dominio. Las viscosidades en este experimento son: $A_{h}=500$ $\mbox{m}^{2}\mbox{s}^{-1}$, $A_{v}=10^{-4}$ $\mbox{m}^{2}\mbox{s}^{-1}$, $k_{h}=10$ $\mbox{m}^{2}\mbox{s}^{-1}$ y $k_{v}=10^{-5}$ $\mbox{m}^{2}\mbox{s}^{-1}$.Ajuste gravitacional sobre una pendienteEste test pretende validar el comportamiento de los modelos numéricos en regiones donde la batimetría presenta grandes gradientes, pasando de una región en la que el océano presenta profundidades de unos pocos cientos de metros a zonas con profundidades de más de $2000$ m en unas pocas decenas de kilómetros. Como en el ejemplo anterior esta situación ocurre con frecuencia a la salida de los estrechos y si existe un intercambio de agua entre las dos regiones que delimita el estrecho, el agua densa debe caer por la pendiente hacia aguas más profundas.Para esta simulación consideramos un dominio de $200$ km de largo y una profundidad que viene dada por la función \[ H\left(x\right)=h_{min}+\frac{1}{2}\left(h_{max}-h_{min}\right)\left(1+\tanh\left(\frac{x-x_{0}}{L_{s}}\right)\right), \] donde $h_{min}=200$ m, $h_{max}=4000$ m, $x_{0}=100$ km y $L_{s}=10$ km, con $0\leq x\leq200$ km. En la siguiente figura mostramos el dominio y el mallado que utilizamos en la discretización de elementos finitos:
Igual que en el ejemplo anterior, las condiciones iniciales simulan dos fluidos con diferentes densidades separados inicialmente por una membrana que se sitúa en $x=60$ km (la diferencia de densidad se simula mediante la temperatura y salinidad exactamente igual que en el ejemplo anterior). En este caso el experimento utiliza las viscosidades $A_{h}=1000$ $\mbox{m}^{2}\mbox{s}^{-1}$, $A_{v}=10^{-4}$ $\mbox{m}^{2}\mbox{s}^{-1}$, $k_{h}=100$ $\mbox{m}^{2}\mbox{s}^{-1}$ y $k_{h}=10^{-5}$ $\mbox{m}^{2}\mbox{s}^{-1}$. El paso de tiempo es $\Delta t=300$ s y utilizamos elementos finitos con polinomios de grado $2$. Ondas internasEn este ejemplo se pretende simular las ondas internas, también conocidas por seiches, que se producen en muchos de los grandes lagos o mares relativamente pequeños y cerrados. Estas ondas se producen por una diferencia de altura en la superficie del mar o del lago o en la superficie que separa dos fluidos de distinta densidad.Para esta simulación suponemos un canal de $6$ m de largo y $29$ cm de altura y dos fluidos con distinta densidad, con una diferencia de densidades de $20$ $\mbox{kg m}^{-3}$. El fluido más denso se situa en la zona inferior del canal tal como muestra el esquema:
es decir, formando un ángulo $\alpha$ respecto de la horizontal, lo que produce las ondas una vez el sistema se deja evolucionar. En concreto, la diferencia de densidad la simulamos con una condición inicial para la temperatura de $20^{\circ}$ C en todo el dominio mientras que para la salinidad utilizamos \[ S_{0}\left(x,z\right)=12+13.2\left(1+\tanh\left(-\frac{z+h-\left(x-3\right)\tan\alpha}{\delta_{\rho}}\right)\right), \] con $h=0.203$, $\alpha=1.5^{\circ}$ y $\delta_{\rho}=0.005$. El mallado está compuesto por $100\times10$ elementos regulares y utilizamos elementos finitos con polinomios de grado $8$, mientras que el paso de tiempo es $\Delta t=0.1$ s. Las viscosidades para este experimento son $A_{h}=10^{-5}$ $\mbox{m}^{2}\mbox{s}^{-1}$, $A_{v}=5\times10^{-6}$ $\mbox{m}^{2}\mbox{s}^{-1}$, $k_{h}=10^{-5}$ $\mbox{m}^{2}\mbox{s}^{-1}$ y $k_{h}=5\times10^{-7}$ $\mbox{m}^{2}\mbox{s}^{-1}$. |

|
|
Contacto: Dpto. Matemáticas del Área Industrial, E.T.S. Ingenieros Industriales.
C/ José Gutierrez Abascal, 2, 28006 Madrid - Spain Tlfn: (+34) 91 06 77369 / fax: (+34) 91 336 3001 / email: pedro.galan@upm.es |