Líneas de Investigación

• Análisis Numérico
  La herramienta matemática conocida como Análisis Numérico puede definirse como la rama de las matemáticas encargada de la resolución, mediante aproximación numérica, de problemas que no pueden resolverse (o son difícilmente resolubles) mediante procedimientos analíticos, y donde los errores en las aproximaciones obtenidas pueden ser controlados mediante teoría matemática. Son especialmente relevantes las aplicaciones a problemas relacionados con las geociencias y la ingeniería.
• Método de Elementos Finitos
  El Método de Elementos Finitos se utiliza principalmente como discretización en espacio para un gran número de Ecuaciones en Derivadas Parciales. En los últimos años se ha venido desarrollando éste método utilizando polinomios de alto orden por su gran respuesta en problemas cuya solución sea regular utilizando pocos grados de libertad.
• Esquemas Semilagrangianos y Lagrange-Galerkin
  Estos esquemas basados en las curvas características, tienen muy buenas propiedades de estabilidad en Ecuaciones en Derivadas Parciales donde aparecen términos de convección o de advección (como las ecuaciones de Navier-Stokes). Si bien han sido clasificados históricamente como esquemas que producen difusión numérica, combinados con discretizaciones con polinomios de alto orden han demostrado ser esquemas muy poco difusivos.
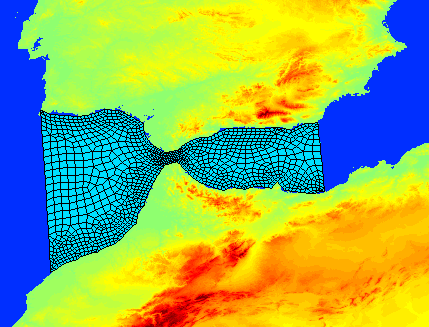
• Aplicaciones: modelos de circulación del océano
  El océano es un fluido, y por tanto puede estudiarse mediante las ecuaciones de Navier-Stokes, en el que además las diferencias de densidad son especialmente relevantes en su dinámica. Si bien históricamente la inmensa mayoría de los modelos numéricos desarrollados utilizan el Método de Diferencias Finitas, recientemente se han empezado a desarrollar modelos basados en el Método de Elementos Finitos que ofrece la versatilidad de las mallas no estructuradas, especialmente relevante para este tipo de problemas.